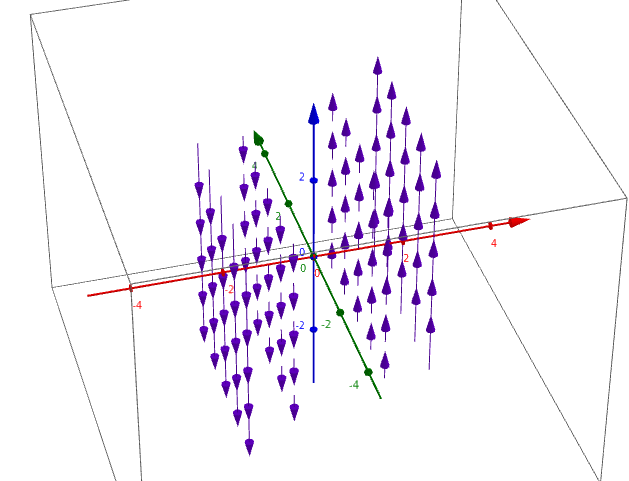
38 sketch the vector field f by drawing a diagram like this figure. f(x, y, z) = −k
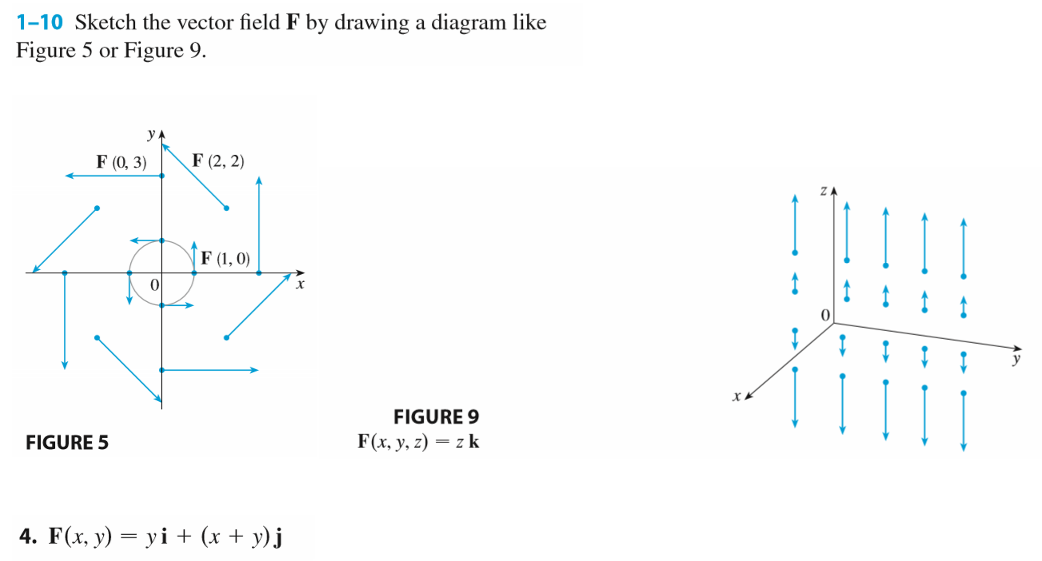
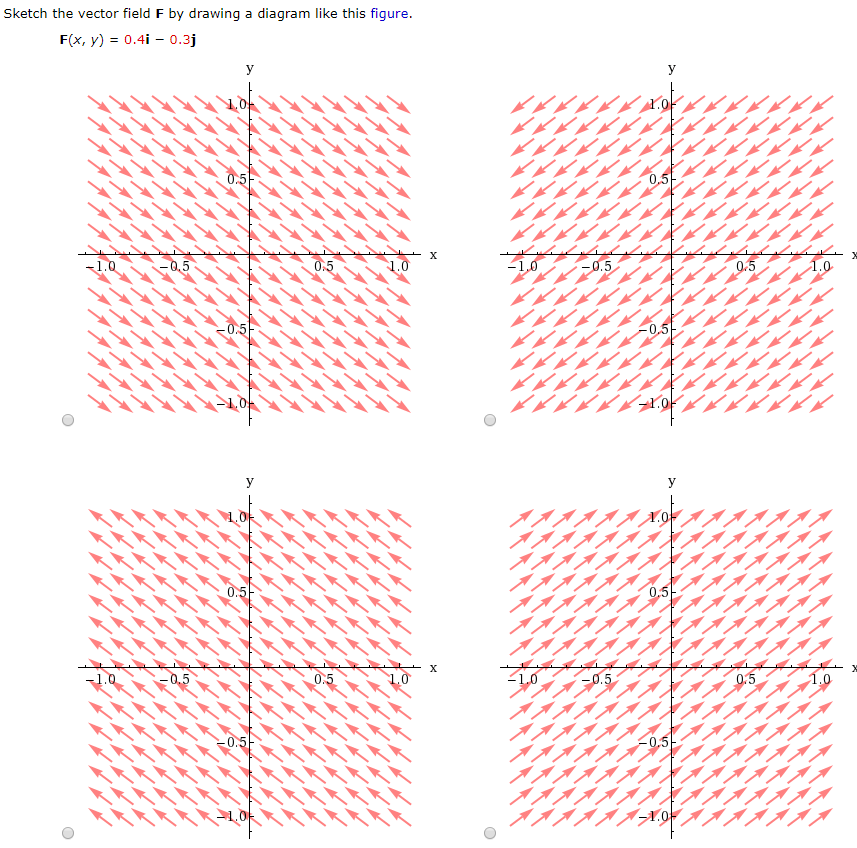
To sketch the phase plane of such a system, at each point (x0,y0)in the xy-plane, we draw a vector starting at (x 0 ,y 0 ) in the direction f(x 0 ,y 0 )i+g(x 0 ,y 0 )j. Definition of nullcline. Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. F (x, y) = 0.3 i − 0.4 j. Step-by-step solution. 100% (38 ratings) for this solution. Step 1 of 5. Consider the vector field. Need to sketch the vector field. Clearly we can observe that the given vector field is a constant vector field so at every point , we draw the ...
The unit vectors along the Cartesian coordinate axis x, y and z are i, j, k, respectively The symbol e n will be used to indicate a unit vector in some n-direction (not x, y, nor z) Any vector can be represented as a multiplication of a magnitude and a unit vector A =Ae n = A e n B =−Be n = − B e n A is in the positive direction along n B ...

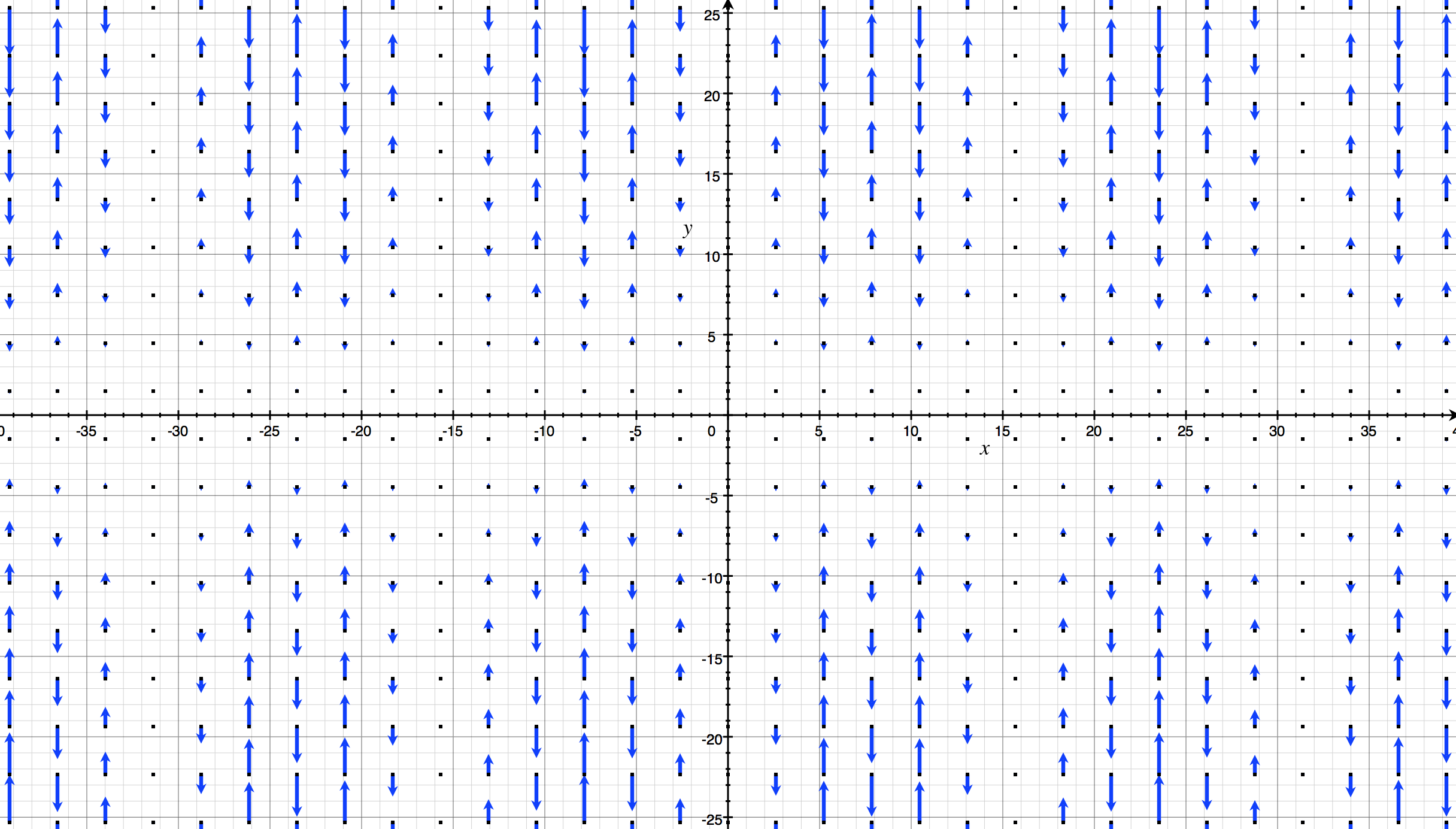
Sketch the vector field f by drawing a diagram like this figure. f(x, y, z) = −k
agram in Figure 16. Solution: Let f(y) = y(4 − y) − k, where k is a parameter that controls the harvestingrate per annum. A phase line diagramis made for each relevant value of k, by applying Theorem 3 to the equilibrium points. First, the equilibria are computed, that is, the roots of f(y) = 0: y2 −4y +k = 0 Standard quadratic form of f ... 110 Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. F(x,y,z)=yi. Calculus, James Stewart 8th edition; 16 Vector Calculus; 1. 16 Vector Calculus 16.1 Vector Fields This chapter is concerned with applying calculus in the context of vector fields. A two-dimensional vector field is a function f that maps each point (x,y) in R2 to a two- dimensional vector hu,vi, and similarly a three-dimensional vector field maps (x,y,z) to
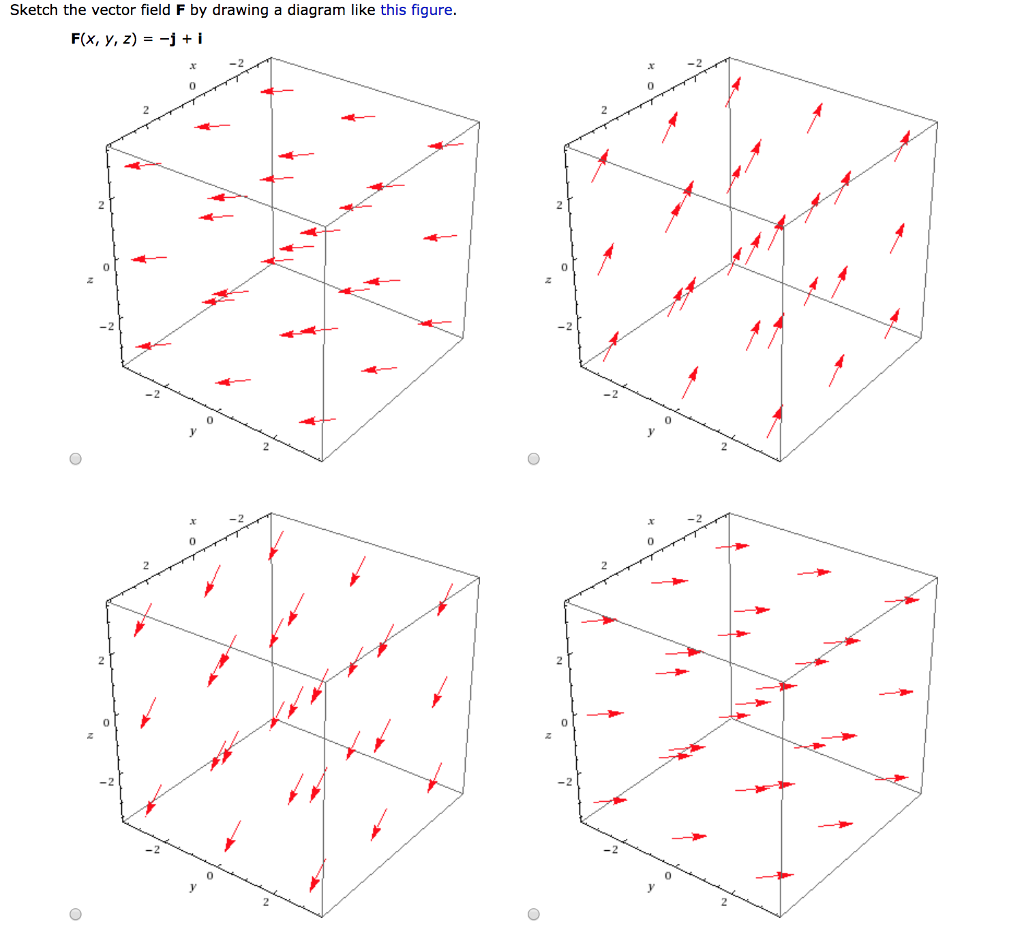
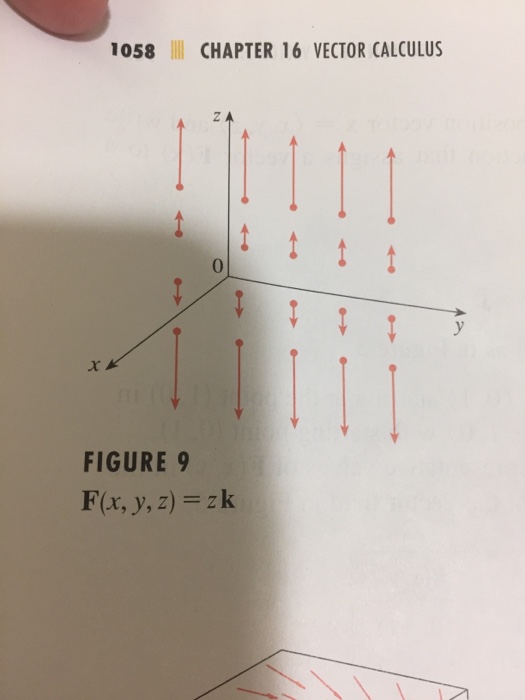
Sketch the vector field f by drawing a diagram like this figure. f(x, y, z) = −k. The unit vectors i, j, and k act in the x-, y-, and z-directions respectively. So in our diagram, since we have a unit cube, OA = i OC = j OS = k . From the diagram, we see that to move from B to S, we need to go −1 unit in the x direction, −1 unit in the y-direction and up 1 unit in the z-direction. Since we have a unit cube, we can write: x-axis. In the drawing below and to the left we see two vectors u and v that are added, and then the vector u+v is reflected across the x-axis. In the drawing below and to the right the same vectors u and v are reflected across the x-axis first, then the resulting vectors Tu and Tv are added. u v u +v T(u+v) y x u v Tu Tv Tu+Tv) y x Note ... Question: Sketch the vector field F by drawing a diagram like this figure. F(x, y, z) = −j + i. This problem has been solved! See the ... CONSERVATIVE VECTOR FIELD A vector field F is called a conservative vector field if it is the gradient of some scalar function—that is, if there exists a function f such that F = . In this situation, f is called a potential function for F. Let's assume that the object with mass M is located at the origin in R3. For instance, M could be the mass of the earth and
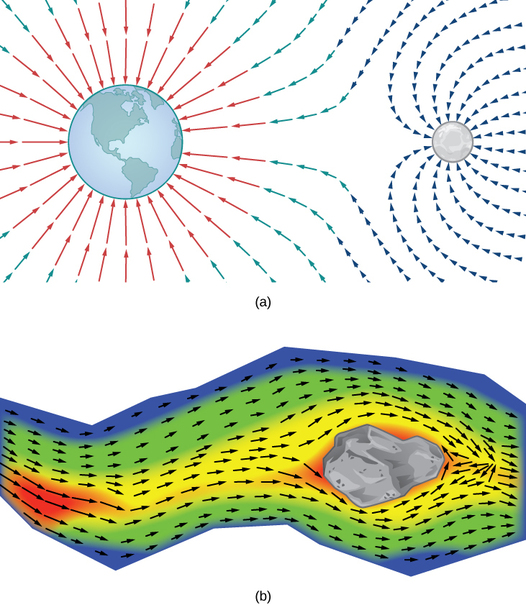
If (x, y, z) (x, y, z) is a point in space, then the distance from the point to the origin is r = x 2 + y 2 + z 2. r = x 2 + y 2 + z 2. Let F r F r denote radial vector field F r = 1 r 2 〈 x r, y r, z r 〉. F r = 1 r 2 〈 x r, y r, z r 〉. The vector at a given position in space points in the direction of unit radial vector 〈 x r, y r, z ... The flow lines (or streamlines ) of a vector field are the paths followed by a particle whose velocity field is the given vector field. Thus the vectors in a vector field are tangent to the flow lines. (a) Use a sketch of the vector field F ( x, y) = x i − y j to draw some flow lines. The end result is known as a vector field. Our interactive demo allows you to enter any function you like for \( g(x,y) \) and \( h(x,y) \). When the page first loads, these functions are set to \[ g(x,y) = ax + by \\ h(x,y) = cx + dy \] The values \( a,b,c \) and \( d \) just simple constants. They are, however, linked to the sliders, which means you can adjust them and watch how the vector ... A vector field is said to be continuous if its component functions are continuous. Example 16.1.1: Finding a Vector Associated with a Given Point. Let ⇀ F(x, y) = (2y2 + x − 4)ˆi + cos(x)ˆj be a vector field in ℝ2. Note that this is an example of a continuous vector field since both component functions are continuous.
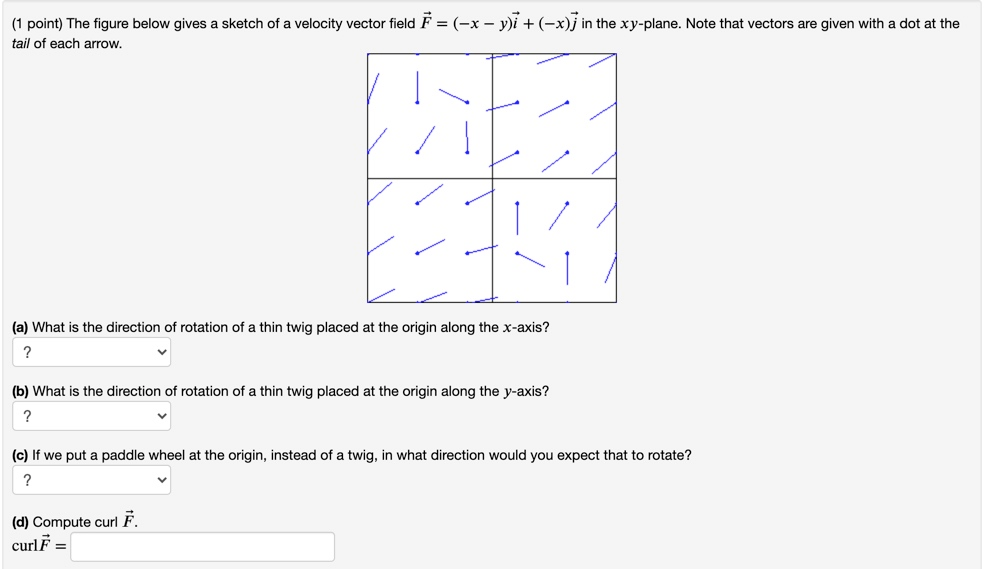
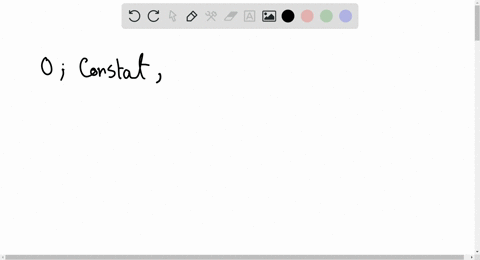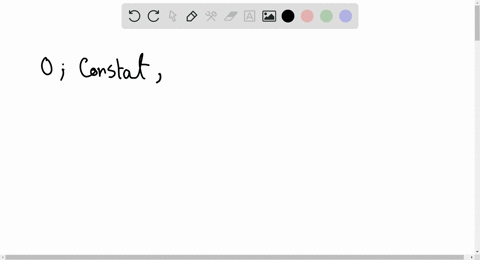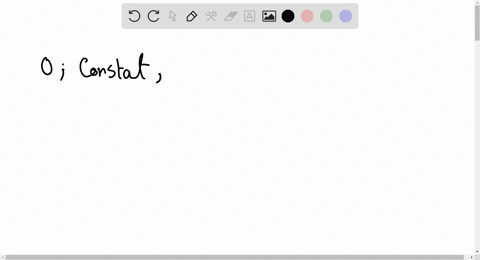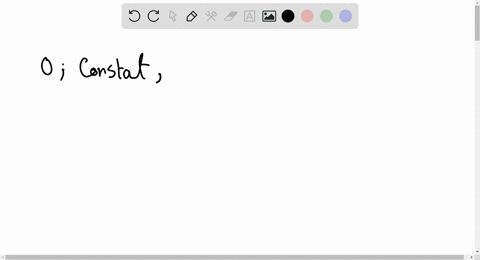
Curl. The second operation on a vector field that we examine is the curl, which measures the extent of rotation of the field about a point. Suppose that F represents the velocity field of a fluid. Then, the curl of F at point P is a vector that measures the tendency of particles near P to rotate about the axis that points in the direction of this vector. . The magnitude of the curl vector at P ... Transcribed image text: ive. 16.1 EXERCISES 1-10 Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. 5 1. F(x, y) = 0.3i - 0.4j 2. F(x, y) = {xi + 3. F(x, y) = -¿i + (y – x)j 4. F(x, y) = yi + (x + y).j 5. F(x, y) = yi+xj Vx2 + y2 6. F(x, y) = yi- xj √x² + y² 7. F(x, y, z) = i 8. F(x, y, z) = zi 9. F(x, y, z) = -yi ... At t = 0, it is located on the x-axis. The angle the particle makes with the positive x-axis is given by where A and B are positive constants. Determine the (a) velocity vector, and (b) acceleration vector (express your answers in polar coordinates). (c) At what time is the centripetal acceleration zero? θ(t)=At 3−Bt Drawing graphs and diagrams using pdfLaTeX. 10 minute read. Published: November 07, 2020. In this post I have collected the options available for embedding vector graphics in LaTeX when using pdfLaTeX. We can always use simple mathematical programs like GeoGebra for 2D and 3D graphs and drawing programs like Google Drawing for diagrams.
Now that we've seen a couple of vector fields let's notice that we've already seen a vector field function. In the second chapter we looked at the gradient vector. Recall that given a function f (x,y,z) f ( x, y, z) the gradient vector is defined by, ∇f = f x,f y,f z ∇ f = f x, f y, f z . This is a vector field and is often called a ...
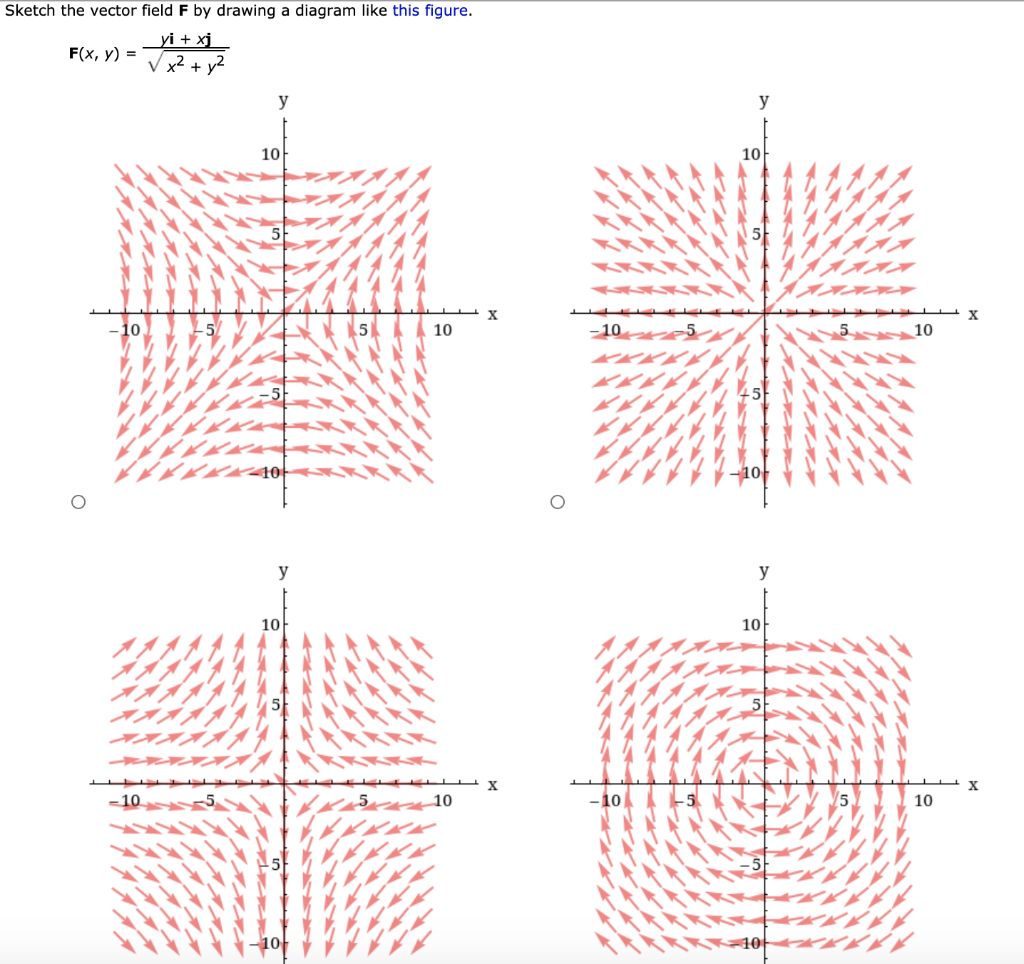
See the answer. See the answer See the answer done loading. Sketch the vector field F by drawing a diagram like this figure. F ( x, y) =. yi − xj. x2 + y2. Show transcribed image text. Expert Answer.
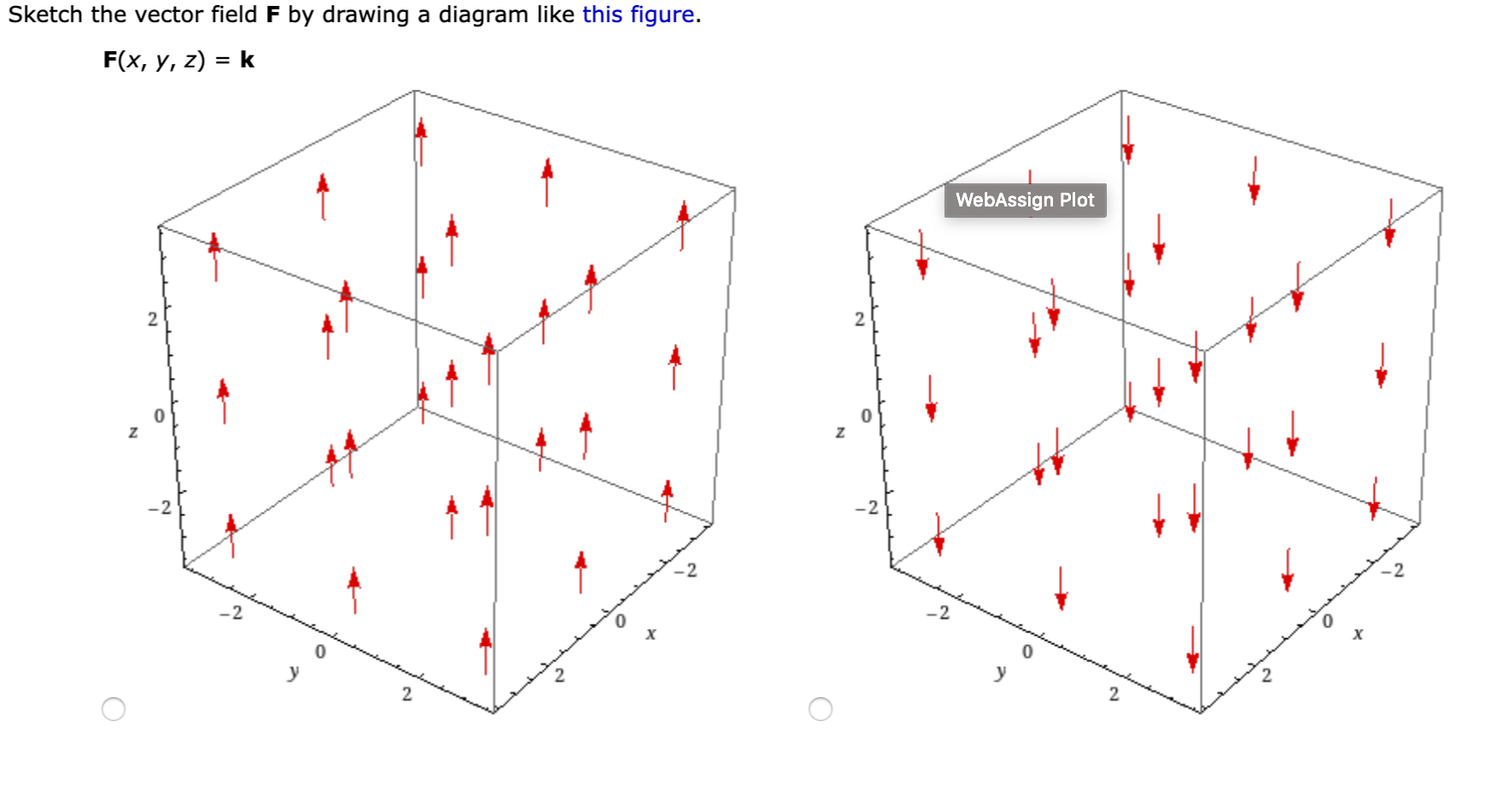
Math. Calculus. Calculus questions and answers. Sketch the vector field F by drawing a diagram like this figure. F (x, y, z) = k WebAssign Plot 2 2 0 0 Z Z -2 2 x 0 0 у 2 2 2 2 0 0 N Z -2 -2 x 0 у у 2 2 WebAssign Plot. Question: Sketch the vector field F by drawing a diagram like this figure.
Question: 10 Sketch the vector field F by drawing a diagram like Figure 5 or ... F(x, y, z) =-yi -3 IV 10, F(x,y,z)=1+k 3 -3 11-14 Match the vector fields F ...
Question: Sketch the vector field F by drawing a diagram F(x, y, z)=yk. Which one is it? I don't understand how to figure this out. · This problem has been ...
Sketch the vector field F by drawing a diagram as in Figure 5. F(x, y, z) = j − k. Step-by-step solution. Step 1 of 4. We need to the sketch the vector ...
Vector Fields. Help Link to this graph. Implicit Equations Vector Fields ©2010 Kevin Mehall ...
Drawing a Vector Field. We can now represent a vector field in terms of its components of functions or unit vectors, but representing it visually by sketching it is more complex because the domain of a vector field is in ℝ 2, ℝ 2, as is the range. Therefore the "graph" of a vector field in ℝ 2 ℝ 2 lives in four-dimensional space. Since we cannot represent four-dimensional space ...
Sketch The Vector Field F By Drawing A Diagram Like This Figure. F(X, Y, Z) = -k. Magnitude of the Magnetic Force The magne… Written By Davis Wallard1976 Tuesday, 9 November 2021 Add Comment Edit. Drawing Tablet With Screen Reddit. Whats a c… Written By Davis Wallard1976 November 09, 2021 Add Comment Edit. Cow Skull With Flowers Drawing. You already know how to draw a skeleton of a head ...
Suppose you know what the graph of a function f(x) looks like. Suppose d 2 R is some number that is greater than 0, and you are asked to graph the function f(x)+d. The graph of the new function is easy to describe: just ... We can use this graph that we know and the chart above to draw f(x)+2, f(x) 2, 2f(x), 1 2f(x), and f(x). Or to write the ...
27 Tangent Planes to Level Surfaces Suppose S is a surface with equation F(x, y, z) = k, that is, it is a level surface of a function F of three variables, and let P(x 0, y 0, z 0) be a point on S. Let C be any curve that lies on the surface S and passes through the point P.Recall that the curve C is described by a continuous vector function r(t) = 〈x(t), y(t), z(t)〉.
science. advanced physics. advanced physics questions and answers. Sketch The Vector Field F By Drawing A Diagram Like This Figure. F (x, Y, Z) = Xk. Question: Sketch The Vector Field F By Drawing A Diagram Like This Figure.
Solution for Sketch the vector field F = <-y, x> Want to see this answer and more? Experts are waiting 24/7 to provide step-by-step solutions in as fast as 30 minutes!*
For this vector field, the x and y components are constant, so every point in has an associated vector with x and y components equal to one. To visualize F, we first consider what the field looks like in the xy-plane. In the xy-plane, Hence, each point of the form has vector associated with it.
Advanced Math questions and answers. Sketch the vector field F by drawing a diagram like this figure. F (x, Y) = 0.4i - 0.3j y . 1.0 IYA -10 MAHARIYANA K -0.5SHIK -0.5F IA MAAAAAAAAAAA LATION MARAT AALASHAVAALAAL TAMILTO.51 HTTAMATTA MAHARHARMATHA सिरसागर 1.0 -1.0 05/ 1.0.
Figure 2.5 (a) When adding vectors by the triangle method, the initial point of w is the terminal point of v. (b) When adding vectors by the parallelogram method, the vectors v and w have the same initial point. It is also appropriate here to discuss vector subtraction. We define v − w as v + (−w) = v + (−1)w.
Note that in projecting a vector onto the xy-plane, the x- and y-coordinates stay the same, but the z-coordinate becomes zero. The formula for the transformation is then T x y z = x y 0 ⇀u x T ⇀u y z Let's now look at the above example in a different way. Note that the xy-plane is a 2-dimensional subspace of R3 that corresponds (exactly ...
Find step-by-step Calculus solutions and your answer to the following textbook question: Sketch the vector field F by drawing a diagram. $$ F(x, y, z) = xk ...
16 Vector Calculus 16.1 Vector Fields This chapter is concerned with applying calculus in the context of vector fields. A two-dimensional vector field is a function f that maps each point (x,y) in R2 to a two- dimensional vector hu,vi, and similarly a three-dimensional vector field maps (x,y,z) to
110 Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. F(x,y,z)=yi. Calculus, James Stewart 8th edition; 16 Vector Calculus; 1.
agram in Figure 16. Solution: Let f(y) = y(4 − y) − k, where k is a parameter that controls the harvestingrate per annum. A phase line diagramis made for each relevant value of k, by applying Theorem 3 to the equilibrium points. First, the equilibria are computed, that is, the roots of f(y) = 0: y2 −4y +k = 0 Standard quadratic form of f ...







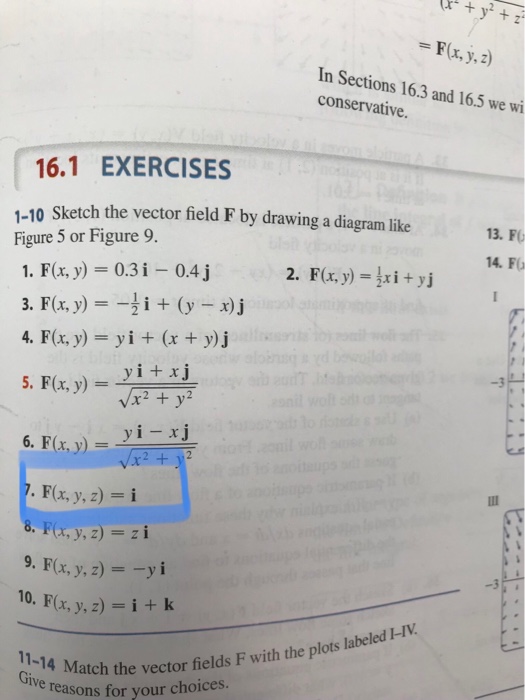




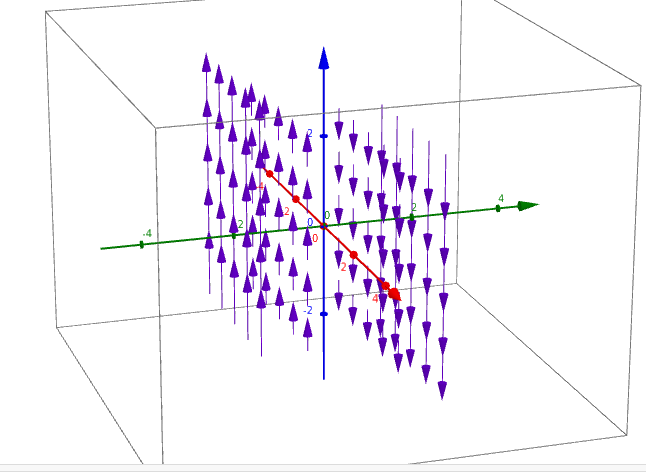

0 Response to "38 sketch the vector field f by drawing a diagram like this figure. f(x, y, z) = −k"
Post a Comment